Timing Your Code

Timing your code is a more complex task you imagine. If the code to run takes long and you are not fond in very precise measurements, then the module time is a very simple way to do it. Otherwise you should use the module timeit. See the two examples below.

from numpy import r_, mat, vstack, eye, ones, zeros
from scipy.linalg import qr
import time
nrEXP = 4
sizes = 2**r_[2:6]
qrtimes = zeros((5,sizes.shape[0]))
k = 0

for n in sizes:
    print 'n=', n
    m = n**2
    A = mat(1.*r_[1:m+1]).T*mat(1.*r_[1:n+1])
    A += vstack((eye(n), ones((m-n,n)) ))
    avqr = 0.
    print(A.shape)
    for k in xrange(nrEXP):
        t1 = time.clock()
        Q, R = qr(A)
        t2 = time.clock()-t1
        avqr += t2

    avqr /= nrEXP
    print avqr
    qrtimes[0,k] = avqr
    avqr = 0.
    for k in xrange(nrEXP):
        t1 = time.clock()
        Q, R = qr(A, mode='full')
        t2 = time.clock()-t1
        avqr += t2

    avqr /= nrEXP
    print avqr
    qrtimes[1,k] = avqr
    avqr = 0.
    for k in xrange(nrEXP):
        t1 = time.clock()
        R = qr(A, mode='r', overwrite_a=True)
        t2 = time.clock()-t1
        avqr += t2

    avqr /= nrEXP
    print avqr
    qrtimes[2,k] = avqr
    avqr = 0.
    for k in xrange(nrEXP):
        t1 = time.clock()
        R = qr(A, mode='r')
        t2 = time.clock()-t1
        avqr += t2

    avqr /= nrEXP
    print avqr
    qrtimes[3,k] = avqr
    avqr = 0.
    for k in xrange(nrEXP):
        t1 = time.clock()
        Q, R = qr(A, mode='economic')
        t2 = time.clock()-t1
        avqr += t2

    avqr /= nrEXP
    print avqr
    qrtimes[4,k] = avqr
    k += 1

import matplotlib.pyplot as plt

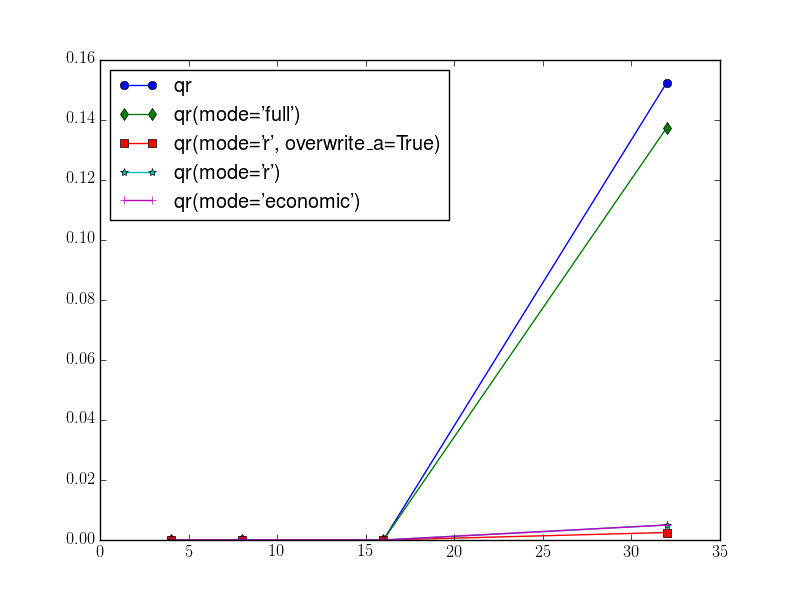
plt.plot(sizes, qrtimes[0], "-o", label=r"qr")
plt.plot(sizes, qrtimes[1], "-d", label=r"qr(mode='full')")
plt.plot(sizes, qrtimes[2], "-s", label=r"qr(mode='r', overwrite\_a=True)")
plt.plot(sizes, qrtimes[3], "-*", label=r"qr(mode='r')")
plt.plot(sizes, qrtimes[4], "-+", label=r"qr(mode='economic')")
plt.legend(loc="upper left")
plt.savefig("time_qr.png")

from numpy import r_, mat, vstack, eye, ones, zeros
from scipy.linalg import qr
import timeit

def qr_full():
    global A
    Q, R = qr(A)

def qr_econ():
    global A
    Q, R = qr(A, mode='economic')

def qr_ovecon():
    global A
    Q, R = qr(A, mode='economic', overwrite_a=True)

def qr_r():
    global A
    R = qr(A, mode='r')

def qr_ovr():
    global A
    R = qr(A, mode='r', overwrite_a=True)

nrEXP = 4
sizes = 2**r_[2:6]
qrtimes = zeros((5,sizes.shape[0]))
k = 0

for n in sizes:
    print 'n=', n
    m = n**2#4*n
    A = mat(1.*r_[1:m+1]).T*mat(1.*r_[1:n+1])
    A += vstack((eye(n), ones((m-n,n)) ))

    t = timeit.Timer('qr_full()','from __main__ import qr_full')
    avqr = t.timeit(number=nrEXP)/nrEXP
    print avqr
    qrtimes[0,k] = avqr

    t = timeit.Timer('qr_econ()','from __main__ import qr_econ')
    avqr = t.timeit(number=nrEXP)/nrEXP
    print avqr
    qrtimes[1,k] = avqr

    t = timeit.Timer('qr_ovecon()','from __main__ import qr_ovecon')
    avqr = t.timeit(number=nrEXP)/nrEXP
    print avqr
    qrtimes[2,k] = avqr

    t = timeit.Timer('qr_r()','from __main__ import qr_r')
    avqr = t.timeit(number=nrEXP)/nrEXP
    print avqr
    qrtimes[3,k] = avqr


    t = timeit.Timer('qr_ovr()','from __main__ import qr_ovr')
    avqr = t.timeit(number=nrEXP)/nrEXP
    print avqr
    qrtimes[4,k] = avqr

    k += 1

import matplotlib.pyplot as plt

v4 =  qrtimes[1,1]* (sizes/sizes[1])**4
v6 =  qrtimes[0,1]* (sizes/sizes[1])**6

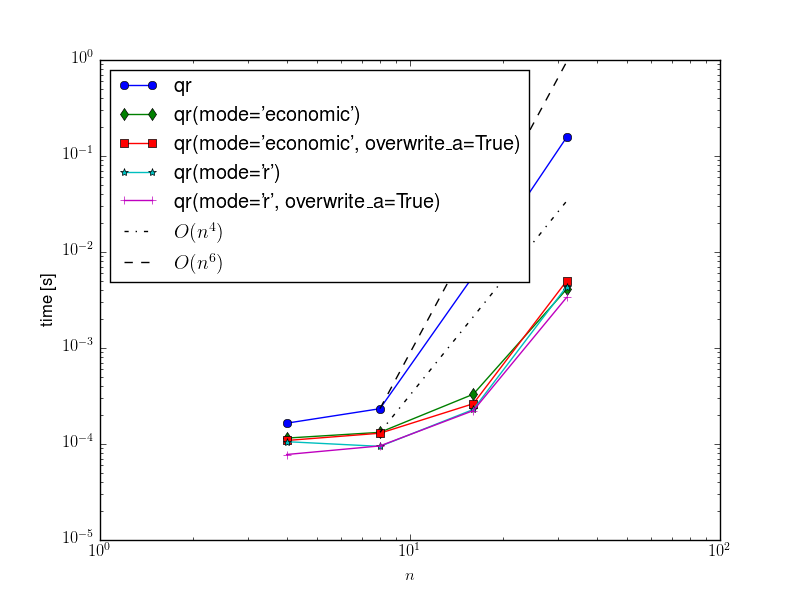
plt.loglog(sizes, qrtimes[0], "-o", label=r"qr")
plt.loglog(sizes, qrtimes[1], "-d", label=r"qr(mode='economic')")
plt.loglog(sizes, qrtimes[2], "-s", label=r"qr(mode='economic', overwrite\_a=True)")
plt.loglog(sizes, qrtimes[3], "-*", label=r"qr(mode='r')")
plt.loglog(sizes, qrtimes[4], "-+", label=r"qr(mode='r', overwrite\_a=True)")
plt.loglog(sizes, v4, "-.k", label=r"$O(n^4)$")
plt.loglog(sizes, v6, "--k", label=r"$O(n^6)$")
plt.legend(loc=2)
plt.xlabel(r"$n$")
plt.ylabel("time [s]")
plt.savefig("time_qr_2.png")