Organizers

Jean Bertoin, Alain-Sol Sznitman, Vincent Tassion, Hugo Vanneuville

Time

Thursday 15:15 - 17:00

Location

UZH Y27 H12 (University of Zürich)

Summary

We study the geometric properties of the level lines of smooth Gaussian functions from the plane to \R (the nodal lines correspond to the specific case of the zero level). The picture below is by Alejandro Rivera (in pink: the points where the random function is positive).

Consider a smooth Gaussian field on the plane and fix some level. We are interested in: (i) the asymptotic behavior of the length of the level set intersected with some domain (are there LLN, CLT, concentration phenomenons?), (ii) the number of connected components of this level set (same questions), (iii) percolation properties (is there an unbounded component? what can we say about the event that a square is crossed by a level line?). The length is a "local" quantity (i.e. we can divide a domain in subdomains, compute the length in each subdomain, and then sum); the number of connected components is not local (even if a local study already gives some information); percolation properties are not local at all.

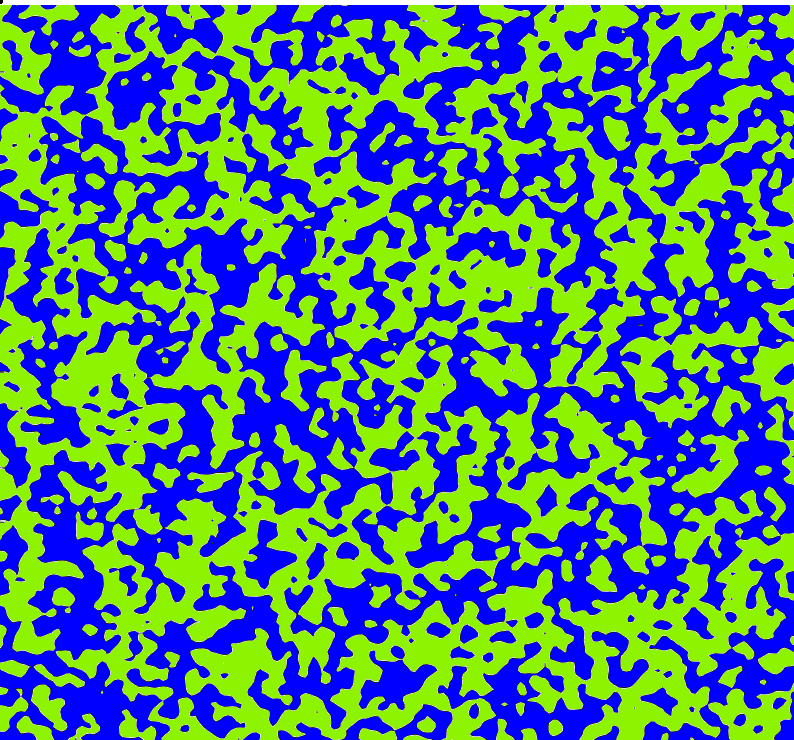
The two main examples of fields that we study are (i) the Bargmann-Fock field which is a random analytic function whose covariance decays very fast to 0 and is positive and (ii) the random planar wave which is a random eigenfunction of the Laplacian and whose covariance does not decay fast to 0 and oscillates around 0. The behavior of these fields are different if we study them from the point of view of the length or of the number of connected components. However, it is believed that they have the same percolation properties asymptoptically.

Below: a simulation of the Bargmann-Fock field (left) by Alejandro Rivera and a simulation of the random planar wave (right) by Vincent Beffara. The blue corresponds to the positive set and the green to the negative set.

     

Plan

First part: Introduction and first results

03/10 and 10/10: Hugo gives an overview on the subject and tries to explain some concentration phenomenons. You can find notes that roughly correspond to these two talks (with a few more things including many references) here. Moreover, you can find here an answer by Matthis to a question asked during the first talk: Let f be a continuous positively correlated field. Is the FKG property true for any monotonic event? (The theorem by Pitt implies the FKG property only for the events that can be approximated by discrete monotonic events.)

17/10: Matthis shows the proof that the number of connected components satisfies a LLN and proves preliminary results for level lines of smooth Gaussian fields. The proof is based on an ergodic theorem. However, since the number of connected components is not a local quantity, one has to study precisely what is the contribution of "boundary terms". You can find notes for this talk here.

24/10: No session.

Second part: Variances and covariance: fluctuations and spatial mixing

31/10: Maximilian discusses Wiener chaoses and CLTs for the length of the nodal lines. The Wiener chaos expansion is an L^2 expansion of functionals defined on a Gaussian space. For the RPW, the length of the level lines is concentrated in the 2nd Wiener chaos if the level is different from 0 and in the 4th Wiener chaos in the nodal case. This phenomenon is called Berry's cancellation and helps proving CLTs: it seems easier to prove CLTs for the projections on specific Wiener chaoses than for the whole quantities.

07/11: We have a guest: Alejandro talks about quasi-independence for nodal lines. General techniques give formulas for covariances of events in terms of point to point covariances and of probabilities of "pivotal events". When the covariance function of the field decays sufficiently fast, this enables to prove quasi-independence results for "topological events" (e.g. percolation events) measurable respectively with respect to the field in two macroscopic boxes at macroscopic distance from each other.

14/11: Benedetta explains the proof of lower bounds for the fluctuation of the number of connected components: for many levels, the fluctuation of the number of connected components of the level set in a box of size R is at least of order R for the Bargmann-Fock field and at least of order R^{3/2} for the random planar wave. Let N_u(R) be the number of connected components of the u-level set in a box of size R and remember that this satisfies a LLN. The proof has two steps: first, proving a lower bound on the fluctuation of N_u(R)-N_{u+a_R}(R) for some well chosen small number a_R (which is possible if the constant in the LLN has non-zero derivative in u); second, proving that the distance in total variation between N_u(R) and N_{u+a_R}(R) is very small.

21/11: No session.

28/11: No session.

Third part: Percolation

05/12: Laurin explains the proof of RSW estimates for models that satisfy the FKG inequality and spatial mixing properties. In the context of smooth Gaussian fields, the question is the following: how can we show that, even if R is very large, the probability that a rectangle of size R is crossed by a nodal line is non negligible? How do the quasi-independence properties help us to prove such a result?

12/12: Daniel shows the proof of phase transition phenomenons for percolation of excustion sets of planar smooth Gaussian fields. We saw last week that, when the level equals 0, the probability of the crossing of a rectangle of a given shape is uniformly bounded away from 0 and 1. Daniel explains why this is not the case at other levels. More precisely: this probability goes to 1 if the level is greater than 0 and goes to 0 if the level is less than 0. The proof presented here uses noise sensitivity ideas.